


Next: Statistical Measures
Up: Reaction Time Mean and
Previous: The Correlation between Mean
According to the Poisson-Erlang model, expectation and variance are as
follows:
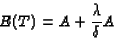 |
(6) |
and
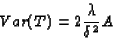 |
(7) |
Taking the natural logarithm of both sides one obtains:
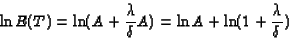 |
(8) |
and
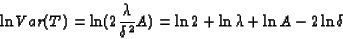 |
(9) |
The logarithm of the variance is a linear function of the logarithm
of the parameters A, 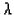 and
and 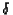 .
However this is not the case with respect
to the logarithm of the expectation. However, the difference between
the expectation E(T) and the real total working time A:
E(T)-A, is a linear function of the log of the PE-parameters.
So, according to the PE model, the correlation across subjects
between
.
However this is not the case with respect
to the logarithm of the expectation. However, the difference between
the expectation E(T) and the real total working time A:
E(T)-A, is a linear function of the log of the PE-parameters.
So, according to the PE model, the correlation across subjects
between
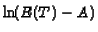 and
and
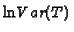 is linearly dependent on the log parameters
is linearly dependent on the log parameters
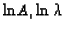 and
and
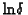 .
This correlation can now easily be described in terms of the
variances and covariances of these variables across subjects.
However, this is a correlation between true scores. In actual practice
only observed scores (estimates)
for
.
This correlation can now easily be described in terms of the
variances and covariances of these variables across subjects.
However, this is a correlation between true scores. In actual practice
only observed scores (estimates)
for
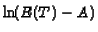 and
and
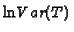 are available. Moreover,
are available. Moreover,
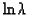 and
and
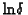 are latent variables. Therefore,
the decision was made to use structural equation modeling to test
the above mentioned linear equations using the
computer program EQS (see Bentler, 1989).
are latent variables. Therefore,
the decision was made to use structural equation modeling to test
the above mentioned linear equations using the
computer program EQS (see Bentler, 1989).



Next: Statistical Measures
Up: Reaction Time Mean and
Previous: The Correlation between Mean
AHGS VAN DER VEN
2002-01-14