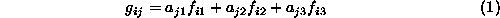
One might argue, that, in intelligence tests, many factors play a role in the realization of the final test score. In that case g, what ever it might mean, must be a composite of more than one underlying factor. The question arises, how, at the same time, the correlation matrix could still be uni-factorial. According to Spearman the solution for this problem could be as follows:
"There are, however, certain special cases where g does admit of resolution into a plurality of sub-factors ... say, for example, ability and zeal. If in all tests the respective influences of these two always remained in any constant ratio, then both could quite well enter into g together; for the tetrad equation would still be able to hold." (Spearman, 1927, p. 93).For example, in the case of three latent sub-factors (e.g. ability, zeal and practice) one might have:
Suppose, however, the following equalities hold:
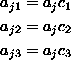
Then the ratios 
, with p = 1, 2, 3 and q = 1, 2, 3
are all constant across tests.
One may write:
The term between brackets represents one factor
The weights 
are independent of the tests.
The factor 
is identifiable, the factors
, 
and 
, however, are not.
One could consider this idea of a plurality of underlying factors
as a rather contrived explanation. However, in the next section an
examlple will be discussed, in which many unidentifiable factors
play a role, while a unifactorial solution still holds. The example
is taken from the game of golf. Everybody will agree, that proficiency
in the game of golf is determined by many factors. However, it will
be shown that factor analysis always results in one factor.
It was on purpose, that the example was taken from a different
domain than that of mental ability testing. Sometimes the pros and cons
of a method are better demonstrated, when the method is appled in a
domain, which is more easy to understand.
